To add locational damage to Skyrim one needs to do math. There's no alternative since the onHit event that is exposed when a target is struck does not include any coordinates of impact nor does it include hit box enumerations. It would of course be better if Papyrus and the underlying physics engine (Havok in this case) exposed which part of the skeletal mesh was affected when reporting on a collision; the onHit event is merely an event generated for a collision. Maybe we can hope Skyrim SE improves Papyrus and adds this functionality.

So we don't know anything other than a target was struck by a certain attacker when this event fires. This means that during the onHit event we need to compute what portion of the target's body was struck based on the assailant's viewing angle and position. The result is a series of cutoffs in degrees that represent each possible hit zone:

	headZone = atan(...) to degrees;

	neckZone = atan(...) to degrees;

	shoulderZone = atan(...) to degrees;

	chestZone = atan(...) to degrees;

	groinZone = atan(...) to degrees;

	legZone = atan(...) to degrees;

For example, if higher degrees is looking upwards and headZone results in 30 degrees and your incident angle is 32 degrees we would then have a head-shot. Note that Skyrim (along with every game) has its own particular conventions for the coordinate system. Increasing the angle positively is not necessarily looking upwards.

C++ Land

On the surface this would normally not be considered computationally intensive; the issue however is that we are in the scripting engine domain. LD competes with a host of other mods for resources. And all code that executes runs in a perfectly safe environment; fatal exceptions are exceedingly rare and this protection comes at a cost. Even more, we want locational damage to support big battles with many actors (as best as we can).

There is one method of speeding up the computations however, Bethesda's help notwithstanding. SKSE allows for user-made plugins that run as native code in C++. These plugins are executed outside the Papyrus scripting engine as native code, in a dangerous and potentially crash-inducing manner. A crappy diagram is shown below to summarize this:

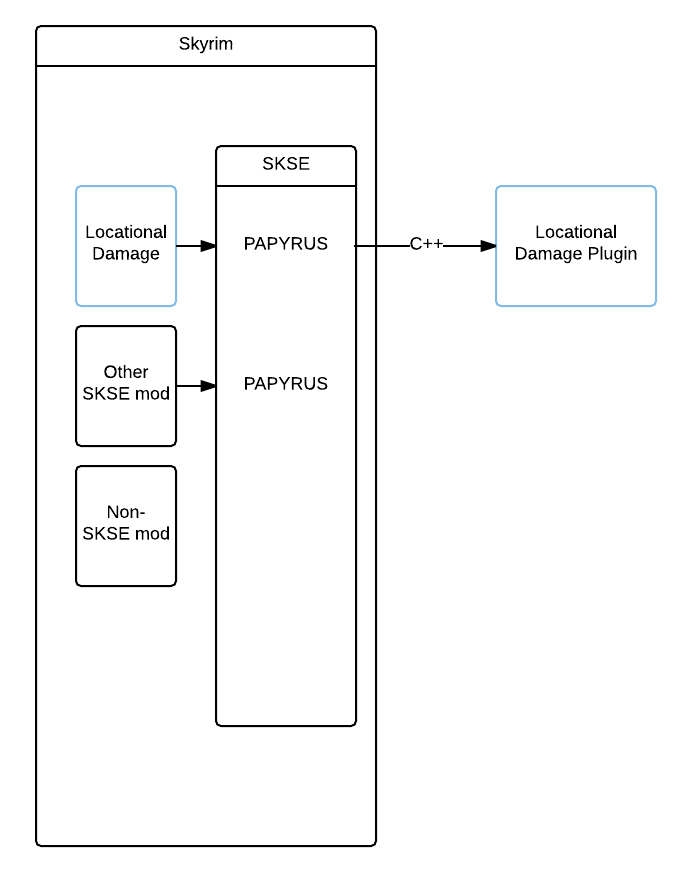
There's an excellent example here by xanderdunn that I used to get started with making my own SKSE plugin. After getting some solid advice on reddit I removed the exports.def file from my configuration and added dllexport qualifiers to the two required SKSE functions in main.cpp.

I needed to get a long list of floats and integers to my plug-in. The provided SKSE headers only include macros for functions of up to ten arguments but this is not enough. So instead we have to use Arrays to be able to pass the full number of arguments from Papyrus to SKSE. These Arrays are then cracked open and moved into structs to keep things organized.

UInt32 SKSEWrapper(StaticFunctionTag *base, VMArray<float> d, VMArray<float> a);

UInt32 someFunction(SomeData d, MoreData a);

A bare bones example on GitHub demonstrating how to set up an SKSE plugin to use Array inputs as in the above snippet can be found here.

The end result is an SKSE plugin written in C++ that takes in several Arrays - filled with angles, coordinates, and scale factors - and outputs a hit zone. The plugin function GetHitZone is invoked in Papyrus:

hitzone = GetHitZone(dimensions, angles, positions, states)

where all the parameters are Arrays.

Approximations

But there's more. If we take a good look at what Locational Damage does in the onHit event, it becomes clear that performance degradation is likely accumulating in the trigonometry calls:

• arctan
• arcsin

These calls are probably using a standard library, which is optimized for the highest accuracy and performance (a good thing!). But for this purpose do we really need maximally accurate results? Put another way- it's highly unlikely anyone will care if an arrow to the knee results in a foot strike vs a leg strike. Even a 5% error, considered intolerable in many other applications, is perfectly ok here. It also helps that the scripted effects are generally consistent and similar between adjacent hit zones.

With that said, this is a textbook case for using approximation functions for the trigonometric calls.

arctan approximation

There exists a paper well beyond my mathematical abilities known as “Efficient approximations for the arctangent function” (Rajan, Inkol, Joyal May 2006) containing a fast atan algorithm implemented in C:

double FastArcTan(double x) { return M_PI_4*x - x*(fabs(x) - 1)*(0.2447 + 0.0663*fabs(x)); }

Don't be fooled by the brevity: there is no doubt that a significant amount of work went into the derivation and testing of this algorithm. It's impressive and useful to us for three reasons:

• It's over 2x as fast as the standard C lib atan
• It has a maximum error slightly less than 1/10th a degree
• It has a usable range of -1 rad to 1 rad

Remember that in this mod atan is called every time a target is hit, and often more than once.

The above positives make this approximation a win for us across the board. We can be reasonably certain it's faster than whatever Papyrus is using for atan. We can be sure that the error is so small that it is all but guaranteed to go unnoticed by the user. And finally the effective range encompasses the vast majority of calculations LD will do (how often are you aiming directly up to hit something?).

arcsin approximation

It's not as easy to find a cooked arcsin approximation. I struggled trying to find a polynomial approximation that minimizes error across the entire range of values and doesn't require range reductions (it's not trivial to benchmark functionality in Papyrus, so I need to be convinced I'm getting speed-ups out of the box). I settled on a Taylor series approximation presented here by Peter K. The issue with Taylor series approximations is that the error gets astronomically worse at the bounds and for most applications this is a problem. However, I went with it anyway as a stop-gap solution until I find or derive something better. The benefit of the approximation below is that it is fast:

function y = arcsin_test3(x) y = x.*(1+x.*x.*(1/6+ x.*x.*(3/(2*4*5) + x.*x.*((1*3*5)/(2*4*6*7))))) endfunction

It is probable that in the next iteration I will put together a function that distributes the error evenly across all inputs; this will most likely be accomplished through the use of a Chebyshev approximation.

So that's it for the three fixes that went into the LD Stability Patch, with roughly 50% the effort going towards performance and 50% going towards stability. Reminder: go here to get a beta mod file on Nexus that incorporates all of the changes. Back up your saved game before installing this mod! Installation with Mod Organizer is trivial; just add the archive as-is. With NMM and manual installations you may need to copy the included SKSE plugin into your Skyrim\Data\skse\plugins directory. I'm going to continue my testing and await a modding apocalypse in October from the release of Skyrim Special Edition.